Understanding Memorization via Loss Curvature

Language models memorize substantial parts of their training data. For example, prompting Llama 3.1 70B with Chapter ONE:⏎THE BOY can generate the entirety of Harry Potter and the Sorceror's Stone near-verbatim with high probability.

From a certain point of view, it's not that surprising that a system trained as a next-token predictor will end up memorizing sequences of tokens. But that's a lot of verbatim memorization!

And many fundamental questions about memorization in models remain mysterious: how are these “memories” stored? Are they localizable in model weights? Do they share common structure? How important is memorization to model capabilities?

As a topical example of the latter question, consider the hypothesis put forth by Andrej Karpathy in his interview on Dwarkesh Podcast:

One thing [agents are] not very good at is going off the data manifold of what exists on the internet. If they had less knowledge or less memory, actually maybe they would be better. […] I actually think we need to figure out ways to remove some of the knowledge and to keep what I call this cognitive core.

Our new research makes headway on many of these fundamental directions.

By analyzing the curvature of a model's loss landscape, we can disentangle the directions in weight space which primarily support memorization from those that support general computation. This lets us selectively edit models to reduce memorization while preserving reasoning capabilities.

Our results reveal a spectrum of model capabilities, with pure memorization on one end and logical reasoning at the other. In between, we find arithmetic, factual recall, and other capabilities that blend memory and computation in different proportions. While some capabilities seem to rely on memorization-heavy directions (including math), others seem to do just fine without them!

Below we provide an overview of our paper: how our method works, what we found, and what those results mean for building better models.

Existing approaches

Many methods for removing memorized information from language models already exist, generally under the label of unlearning.

One recent SOTA unlearning method, which we use as a baseline, is BalancedSubnet (BSN). Given a “forget set” of specific sequences to unlearn, BSN learns a “memory mask” over model parameters to increase loss on the forget set while maintaining performance on clean data.

While effective on targeted sequences, this approach also corrupts sequences that aren't in the forget set. And while it sometimes suppresses untargeted memorization, it doesn't do so consistently. BSN is thus limited by being neither strictly targeted nor consistently general in its effects on the recitation of memorized data.

Our method takes a different approach. Rather than optimizing to forget specific data, we find a general signature of memorization in models, and use it for optimization-free¹ suppression of memorized examples broadly.

¹We use a small set of known memorized data to select hyperparameters, such as where in the model to edit weights and how aggressively to edit. We hypothesize that future work could make this process entirely unsupervised, using only dataset statistics.

Intuitions for Loss Curvature

To understand how we separate memorization from reasoning, we first need to talk about the loss landscape - the loss at every point in weight space.

We usually hear about the loss landscape in the context of training: an optimizer modifies a model's weights, thus traversing weight space and the loss landscape (as in the image above).

Here, we focus on the shape of the loss landscape at a single point in weight space, after a model has already been trained.

In particular, we focus on the curvature at that point along different directions. Consider the right side of the diagram below: the bottom of the basin has high curvature along the red axis, but low curvature along the blue axis. Of course, a real loss landscape is much higher-dimensional - since it's parameterized by every weight - and so exhibits curvature along many more axes.

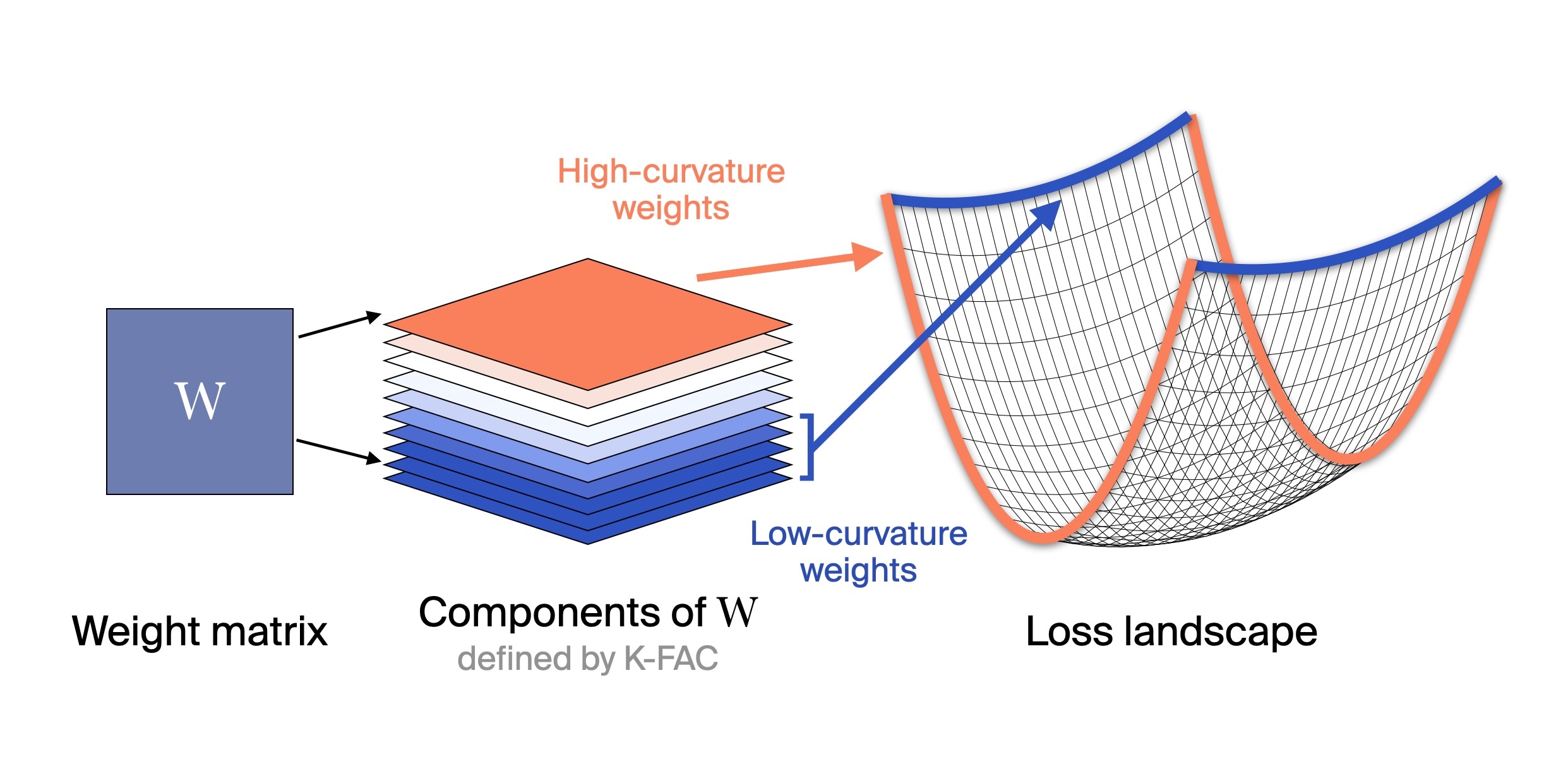
How does this connect to memorization? Curvature here measures how quickly the loss changes when you perturb the weights. Let's say that we compute the loss on a particular example, rather than over all of the training data. Previous work has established that the loss on individual memorized examples has high curvature - i.e., is sharp and brittle (Garg et al. 2023, Ravikumar et al. 2024). If a model has memorized a specific training example exactly, perturbing the relevant weights even slightly breaks that memorization and spikes the loss. The loss landscape for generalizing solutions, by contrast, tends to be flatter - it's robust to small perturbations because generalizing solutions capture broader patterns.

Our work, however, considers the loss over many training examples rather than just one. Counterintuitively, this flips the above relationship on its head. A direction being flat implies that perturbing those weights changes the loss for very few examples, as is the case for memorized data. Meanwhile, directions in weight space that correspond to shared, general computational structures - the mechanisms for attention, composition, reasoning, etc. - exhibit higher curvature because they're used across many examples, and so perturbing those weights changes the overall loss much more.

This means that in the dataset-level view, moderate curvature corresponds to shared computational structures, while low curvature corresponds to memorized content and other rarely-used patterns.

The edit: suppressing memorization through curvature

Our method is mathematically similar to PCA, but instead of finding directions of maximum variance in data, it finds directions that most influence the model's loss.

The approach, which requires only the model and some unlabeled data, has four steps:

1. Collect activation and gradient statistics by running forward and backward passes of the model on a random subset of training sequences.
2. Infer curvature from those statistics using K-FAC, which is an efficient way to approximately discover curved directions.
3. Use that curvature approximation to decompose² a weight matrix, thus identifying which parts are widely used versus narrowly memorized.
4. Zero out the low-curvature components.

See section 5 of the paper for a more detailed description of our method.

So: does this method have the expected effects? Let's see what happens when we apply this edit to real models.

²Here “decompose” means expressing the weight matrix in a different basis (the K-FAC eigenvectors), not a traditional matrix factorization

³While our method is unsupervised in the sense of having no trainable parameters in the traditional sense, we still use the term “training set” for the collection of text used to generate these statistics. Note that this collection of text used for K-FAC is sampled from the training corpus of the model, which is a distinct “training".

Results

In language models

Applying the curvature-based edit to language models produces the results shown below. We compare BSN (the SOTA unlearning baseline) with our method on two validation sets:

• Dolma validation: memorized sequences that both methods had been trained on (for BSN, the forget set; for K-FAC, the “training set” used to generate curvature statistics)
• Historical quotes: memorized sequences that neither method was trained on

The performance difference on these completely unseen quotes suggests the methods identify memorization through different mechanisms.

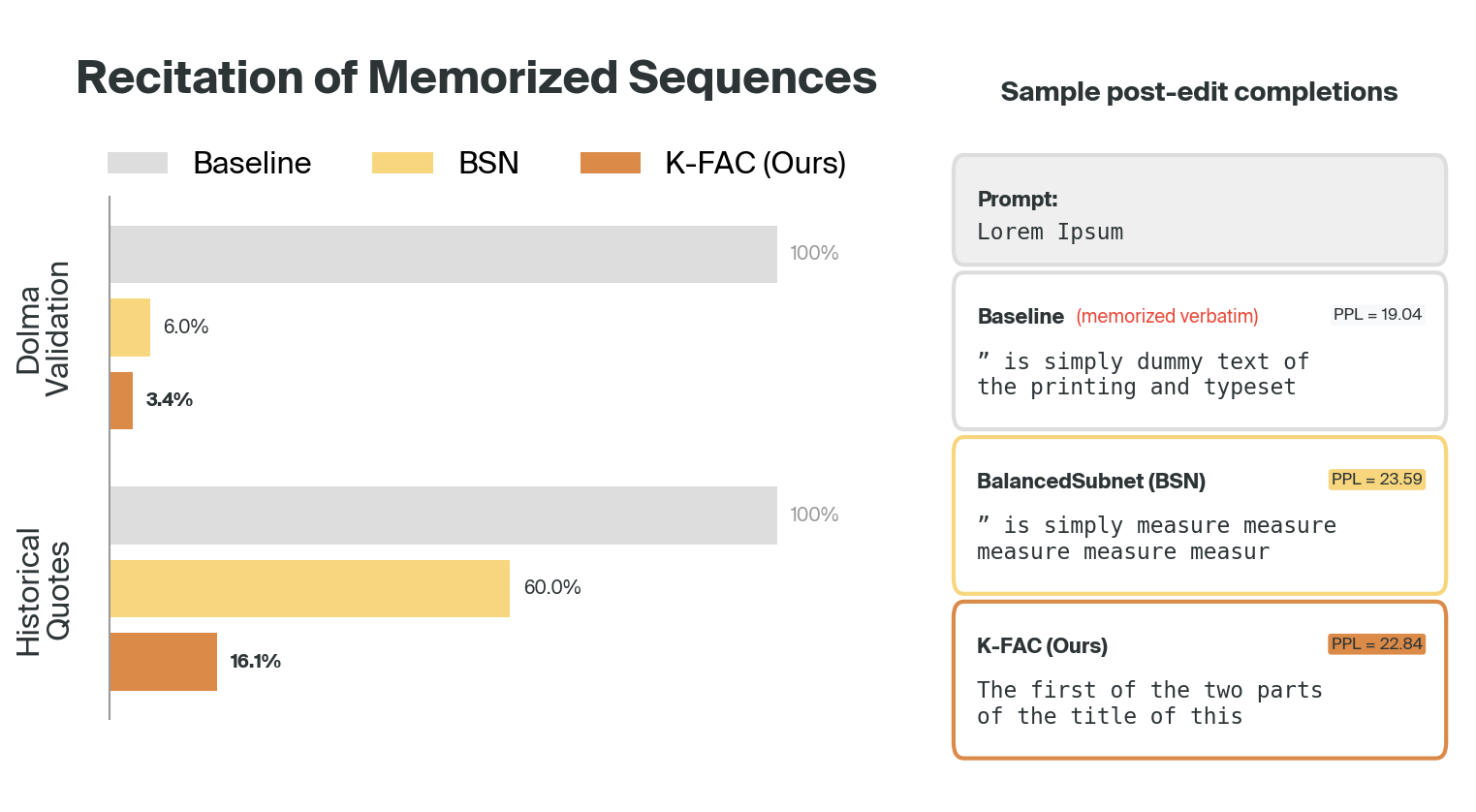
We see that the K-FAC method is significantly more effective at reducing recitation of examples not in the training/forget set. Meanwhile, as we discuss in the next section, performance on tasks involving pure logical reasoning is unaffected, or even improves slightly!

We also see a qualitative difference between the outputs of BSN-edited vs. K-FAC-edited models: the K-FAC completions tend to be more coherent, while retaining perplexity closer to that of the original model.

In vision transformers

We see similar results in vision transformers (ViTs). We trained ViT models with 10% random label noise. Since random labels cannot be accurately predicted via any generalizable rule, this procedure incentivizes the model to memorize those examples.

After applying our edit, memorization of the noised labels drops from 81.6% to 3.5%. Surprisingly, the model recovers the correct labels 66.5% of the time on noised examples (compared to 10.5% before editing), and validation accuracy actually improves from 67% to 71.7%. The edit appears to remove overfit structure, acting as a form of regularization.

From memorization to reasoning: a spectrum of tasks

We tested the edited language models on a range of downstream tasks. Our results show that these capabilities exist along a spectrum, varying in how much they depend on the weight components that our edit removed:

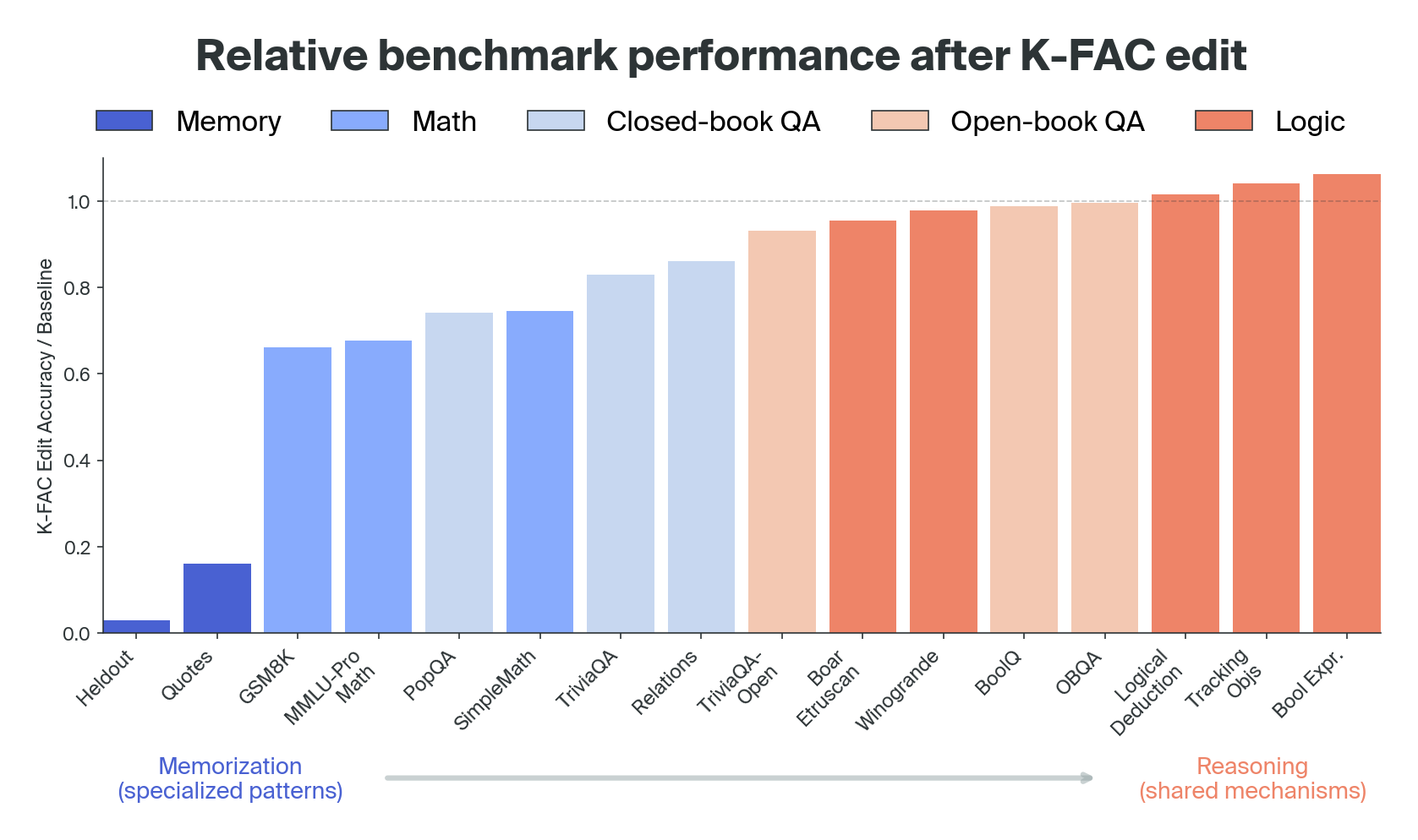
At one extreme, performance on tasks involving pure memorization sharply deteriorates (as expected), dropping to just 3–16% of the original accuracy. At the opposite extreme, logical reasoning tasks remain robust - or even slightly improve post-edit.

In between those extremes lie tasks like math and question-answering. Perhaps surprisingly, some mathematical tasks seem to rely on memorization-heavy structure more than most of the other tasks we tested. When the model solves an arithmetic problem like “30 + 60,” its learnt rule appears to recruit parts of the model that are also used for memorized sequences, so removing those components often disrupts these precise operations.

In the example below from GSM8K, the reasoning chain remains intact, but the model makes an arithmetic mistake in the final calculation. This and similar examples seem to indicate that the reduced performance on math benchmarks comes largely from arithmetic errors. Since solving word problems requires both reasoning (to understand and formalize the question) and calculation, the edited model's poor arithmetic abilities mean it does poorly on the overall math benchmarks - even though its reasoning capabilities are preserved.

Perhaps we shouldn't be so surprised that our edit affects arithmetic so strongly: when doing mental math, humans tend to rely heavily on memorized patterns like multiplication tables, and previous work has identified quite granular features involved in LLM arithmetic which correspond to adding specific ranges of numbers.

Closed-book factual recall is a similar story to arithmetic. While the knowledge that (for example) Paris is the capital of France is not merely verbatim memorization of a specific sequence, it's still a precise and specialized pattern, and skews closer to pure memorization in our method's effects.

These results help us understand the effects and potential limitations of our method.

Conclusion

Our curvature-based edit reduces memorization without needing labeled examples of what to forget. By analyzing the curvature of the loss landscape, we identify weight directions that are rarely activated, and can remove them to suppress memorization naturally.

The method is not yet mature - its simplicity also means it can be heavy-handed in its edits, and some memorized examples might slip through. But it does shed new light on old and fundamental questions about memorization. For example, we characterize the ways different tasks are affected by memorization suppression, giving a granular picture of the role memorization plays in different model capabilities.

We also find regularities in the ways memories are stored: while memorization may or may not live in a particular layer or attention head, large collections of memorized datapoints do seem to live in a common region of the curvature spectrum. Thus, memorization has a recognizable signature, independent of where in the model it occurs.

Our results open up several exciting directions for future work:

• How can the method be made finer-grained? As a naive proposal, could one apply our method and then train a few memorization-heavy yet desirable capabilities back in?
• Can we train models to encode tasks like arithmetic using more robust mechanisms?
• Could we tune models to use more or less memorization at inference time?
• Are there nontrivial “optimal levels of memorization” for different tasks?
• Where do other tasks - e.g., reasoning-heavy advanced math (as opposed to arithmetic) - fall on the spectrum when you apply this technique to more capable models?

We're excited to see more work in this direction!